El principio de Arquímedes es uno de los hallazgos más significativos que nos concedieron los griegos para resolver uno de los más importantes enigmas matemáticos.
Todo comienza con una interesante historia que involucra a Arquímedes, un rey y una corona de oro.
El rey era nada más y nada menos que el rey Hierón, el cual dictaminó que se le fuese fabricada una corona de oro puro y para demostrar que no había sido estafado, solicitó a Arquímedes que le indicara si la corona era completamente de oro o tenía alguna aleación con otro metal, eso sí, Arquímedes no podía romper la corona.
Como en ese tiempo aún no se conocía como calcular el volumen de los objetos con formas irregulares, Arquímedes se tuvo que idear un método para obedecer el mandato del rey.
La leyenda cuenta que mientras Arquímedes se disponía a darse un baño en una tina o bañera, en la que por error llenó con mucha agua, al sumergirse en ella, parte del agua se derramó. En ese momento, comprendió de que dicha situación podía permitirle solucionar el misterio de la corona del rey Hierón; y fue tanta su emoción que desnudo, salió corriendo de la bañera exclamando «¡Eureka, eureka!» (¡Lo he descubierto!).
En ese mismo instante, Arquímedes pudo comprender que estaba presenciando un importante descubrimiento. Y no se equivocaba ya que gracias a él ahora es posible conocer el volumen de sólidos irregulares, haciendo uso del método que luego se denominó como Medición de Volumen por Desplazamiento de líquidos.
Entonces para resolver el enigma, una vez sabiendo el volumen y masa de la corona, Arquímedes lograría hallar la densidad del material que se empleó para fabricar la corona. Si dicha densidad era menor que la del oro, esto indicaba que se había agregado algún otro material menos denso que el oro y de menor calidad.
En busca de la respuesta, tomó un fragmento de plata y otra de oro de igual masa que la corona. Llenó completamente de agua un recipiente e introdujo la pieza de plata y midió la cantidad de agua vertida. Posteriormente realizó lo mismo con la pieza de oro. De esta forma, estableció qué volumen correspondía a la plata y qué volumen correspondía el oro.
Realizó el mismo procedimiento pero ahora con la corona del rey. El volumen de agua que desplazó la corona se ubicó entre medias del volumen de la plata y del oro. Ajustó los cálculos y estableció de forma exacta la cantidad de plata y oro que tenía la corona, demostrando así ante el rey Hierón que el orfebre le había pretendido engañar con la supuesta corona de oro puro.
Ahora bien ¿qué nos establece el principio de Arquímedes?
El principio de Arquímedes señala que “todo cuerpo sumergido dentro de un fluido experimenta una fuerza ascendente llamada empuje, equivalente a la masa del fluido desalojado por el cuerpo”.
Un ejemplo cotidiano que se relacione con este enunciado, lo podemos evidenciar cuando lanzamos un objeto al agua; el objeto se hunde si su masa es mayor que la masa del fluido desplazado. El objeto flota cuando su masa es menor o igual a la masa del fluido desalojado.
Todo lo anterior se relaciona con la fuerza de empuje hacia arriba (ascendente), que recibe todo cuerpo que se encuentra inmerso en agua o en cualquier otro fluido.
¿Cómo se calcula el volumen de sólidos irregulares?
Para determinar el volumen de una roca (o cualquier otro sólido de forma irregular), se debe tomar un cilindro graduado de unos 50 ml o de la graduación que usted tenga a su disposición, y llenarla de agua hasta la marca de 40 ml. Seguidamente, se coloca la roca dentro del agua. Luego que la roca se haya hundido totalmente, el nivel del agua habrá ascendido, desde los 40 ml iniciales a 45 ml, por ejemplo.
La diferencia de nivel determina el volumen de la roca. En este caso sería 5ml la diferencia entre ambos volúmenes.
Volumen del sólido = Volumen final – Volumen inicial
Volumen del sólido (roca) = 45 ml – 40 ml
Volumen del sólido (roca) = 5ml
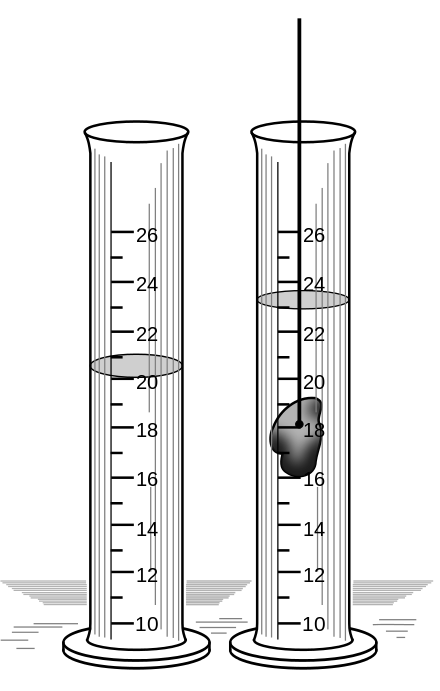
Como la roca no absorbe agua, el espacio que ocupa desplaza el agua hacia arriba y, de esta manera es posible determinar su volumen.
También les puede interesar:
Masa: Propiedades No Características
Volumen: Propiedades No Características