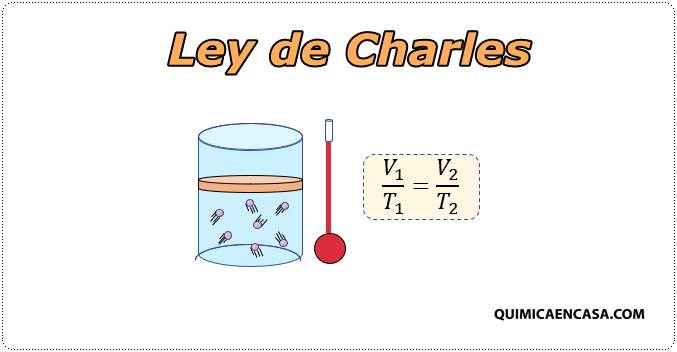
La ley de Charles es una de las leyes de los gases. Esta relaciona el volumen y la temperatura de una cantidad especifica de gas ideal, a una presión constante, a través de una constante de proporcionalidad directa.
Jacques Charles fue un inventor, científico y matemático francés, que para el año 1788 descubrió la ley que hoy lleva su nombre.
Su descubrimiento fue previo al de Louis Joseph Gay-Lussac, quien publicó en 1802 la ley de expansión de los gases. Por lo tanto, hoy en día sus conclusiones probadas han sido denominadas Ley de Charles o de Charles-Gay Laussac como es costumbre cuando se da crédito por investigaciones independientes que arriban a idénticos resultados.
La ley de Charles se puede enunciar de la siguiente manera:
A presión constante, los volúmenes que ocupa una masa gaseosa son directamente proporcionales a las temperaturas absolutas.
La expresión matemática de esta ley es la siguiente: V/T = K; por lo tanto al estar la presión constante, la expresión queda:
V1.T2 = V2.T1
Por ejemplo.
- Cierta masa de un gas, ocupa a presión constante, un volumen de 3,5 litros a la temperatura de 27 °C. ¿Cuál será el nuevo volumen ocupado por el gas a la temperatura de 50 °C?
Datos:
V1 = 3,5 litros
T1 = 27 °C
T2 = 50 °C
V2 = ?
Primeramente, se debe transformar las temperaturas de °C a K. Para ello se le debe sumar 273.
T1 = 27 °C + 273 = 300 K
T2 = 50 °C + 273 = 323 K
Ahora, para hallar el V2 se debe despejar la fórmula principal:
V1.T2 = V2.T1
V2 = V1.T2 / T1
V2 = 3,5 litros. 323 K ÷ 300 K
V2 = 3,77 litros
- Un gas, a presión constante y a la temperatura de 17 °C, ocupa un volumen de 258 ml. Determine la temperatura (Kelvin) necesaria para que el volumen aumente a 520 ml.
Datos:
V1 = 258 ml
T1 = 17 °C
T2 = ?
V2 = 520 ml
V1.T2 = V2.T1
T2 = V2.T1 / V1
T2 = 520 ml x 17 °C ÷ 258 ml
T2 = 34,26 °C + 273 = 307, 26 K